Electron Holography (greek: “holography” = “whole” + “writing”) is a method to measure both the phase and the amplitude of an electron wave function. There are several ways of obtaining this wave function. The most widely known method is probably off-axis electron holography in which the one part of a coherent electron wave passes through the object (or area of electrostatic or magnetic field) of interest and the other part passes through a field-free region (vacuum).

Inline holography reconstructs the phase of the electron wave function from the Fresnel fringes produced by local variations in the phase of this wave function. As an illustration: A local difference in the thickness of the water layer avove the sand in the image above produces Fresnel fringes in the defocused image of the sunlight’s wave function.
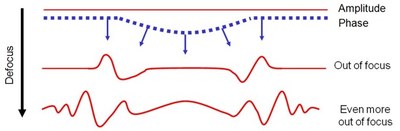
Recording several such patterns at different values of the defocus (or water depth in the above illustration) allows the reconstruction of the complex wave function. This works, even if the wave function is only partially coherent, as long as the spatial coherence properties are known (or can be fitted).
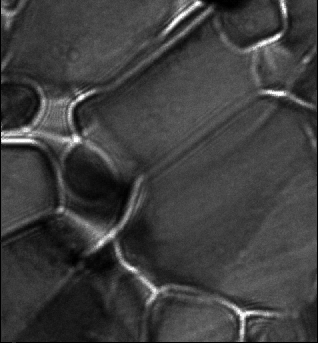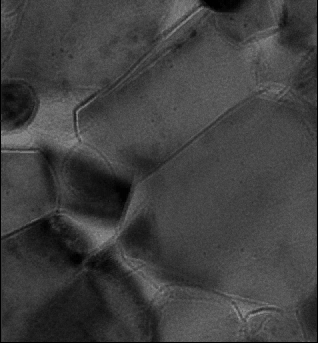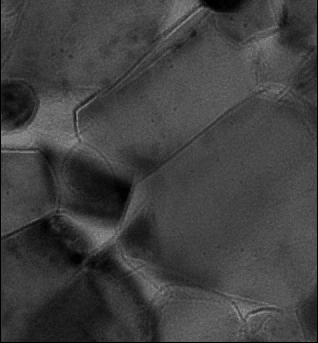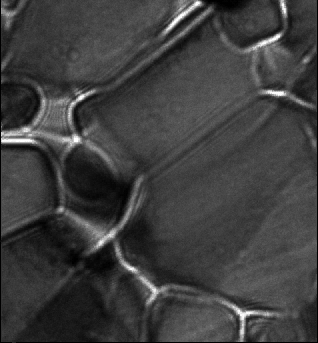
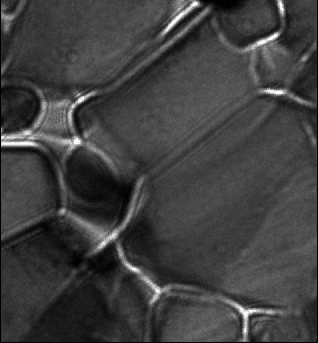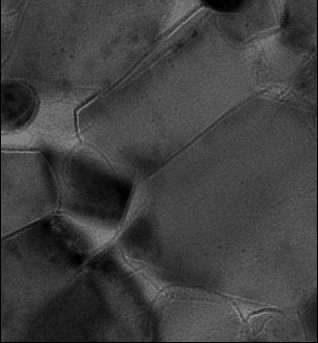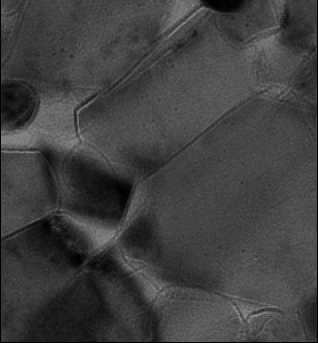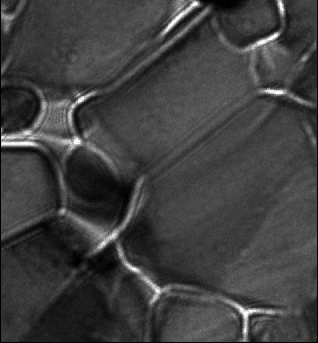
The above animations show a focal series of TEM images of a ceramic. The left series represents the raw experimental data while the movie to the right shows the images after alignment and correction of microscope distortions.

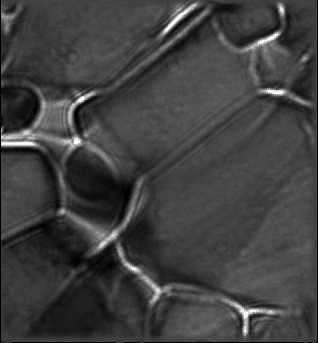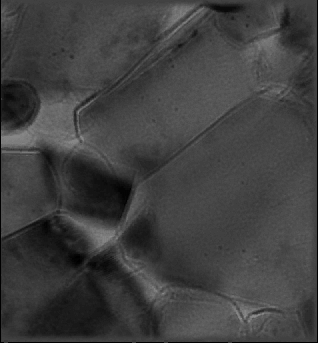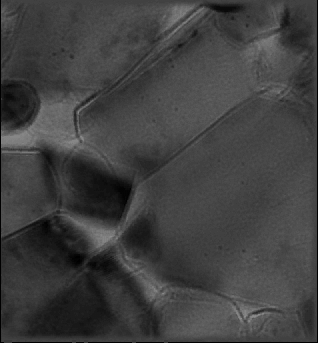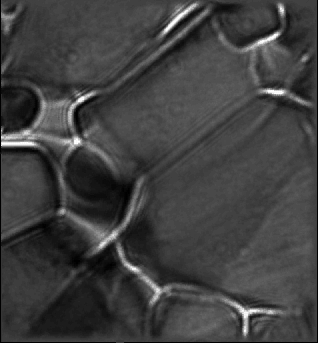
The non-linear inline electron holography full-resolution wave reconstruction (FRWR) algorithm recovers the complex wave function the phase of which is shown to the left. Once this wave function has been reconstructed it is easily possible to simulate the set of defocused images from it. Comparing such simulated defocus series (shown to the right in the above image) provides reassurance that the reconstruction is correct.
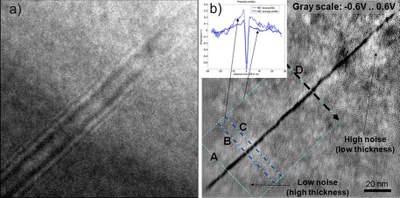
The above image shows the reconstruction of variations in the mean inner potential across a grain boundary in a bicrystal of SrTiO3 by nonlinear inline electron holography. One of the defocused images used for reconstructing the electron wave function is shown to the left. On the right the mean inner potential extracted from the focal series normalized to the specimen thickness is shown. The local specimen thickness has been determined from a separate focal series of the same region but with the sample tilted by 18deg.

In order to reconstruct very low spatial frequency information, i.e. relative phase differences across large distances, it is necessary to go to very large values of the defocus, especially, if a small objective aperture is used. Changing the current in the objective lens by such large amounts changes not only the defocus but also the magnification, image rotation, as well as some other distortions. The above animation shows the effect of the distortions on the image which have been fitted during the reconstruction of an experimental focal series recorded on the Zeiss SESAM. (Distortions were amplified by a factor of 5 for illustration).
Advantages of inline holography over off-axis holography are:
- In inline holography the object wave is the reference wave. There is no need to worry about the reference wave passing through absolutely field-free space.
- This also means that inline holography can be applied anywhere, even far away from the specimen edge.
- Inline holography experiments are very simple. No special hardware is needed. The acquisition can be automated quite easily (see, for example, the FRWR acquisition script).
- If the specimen drifts one can simply replace a long exposure time with several short ones, which can then easily be drift corrected and summed up (this is already implemented in the FRWR acquisition plugin). In off-axis holography the interference fringes remain stationary even if the sample drifts.
- Inline holography also works with very limited spatial coherence (even with a LaB6 source), because there is no need to create a vacuum reference wave which is coherent with the object wave.
- Long exposure times mean usually high signal/noise properties. Also, the less stringent requirements on beam coherence helps in this regard.
For mathematical details please see this recently published manuscript:
C.T. Koch, “A flux-preserving inline electron holography reconstruction algorithm for illumination of partial spatial coherence”, Ultramicroscopy 108 (2008) 141-150